
Download Freebie Pack Here:


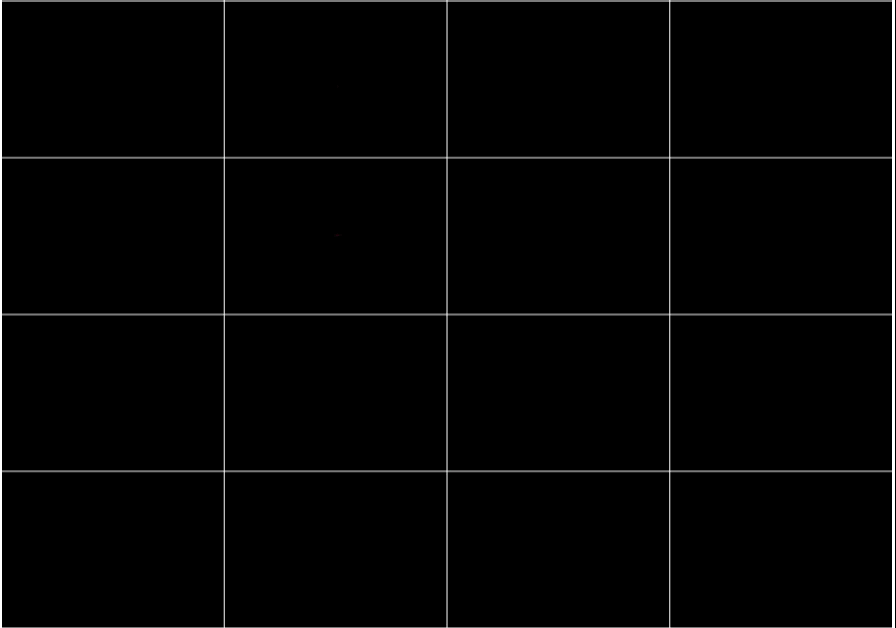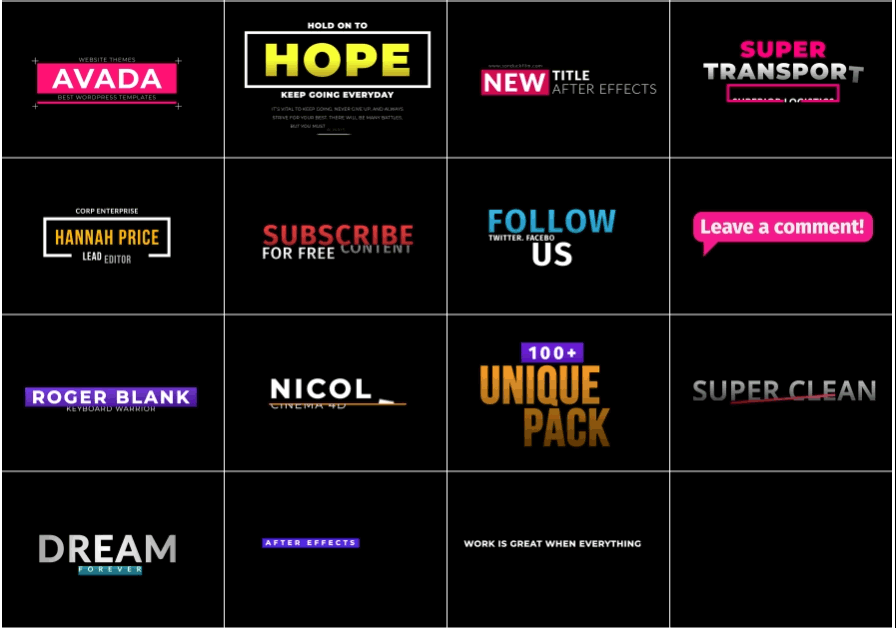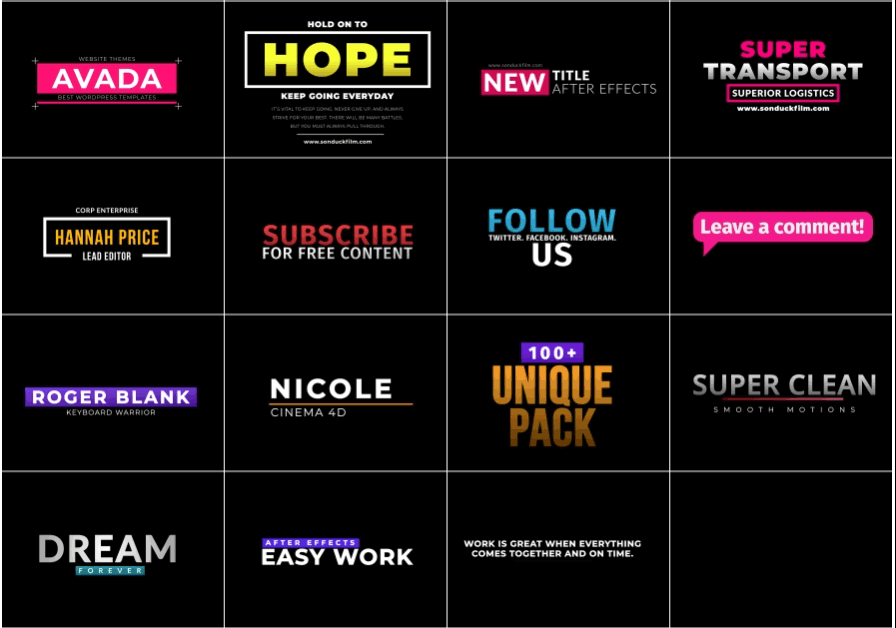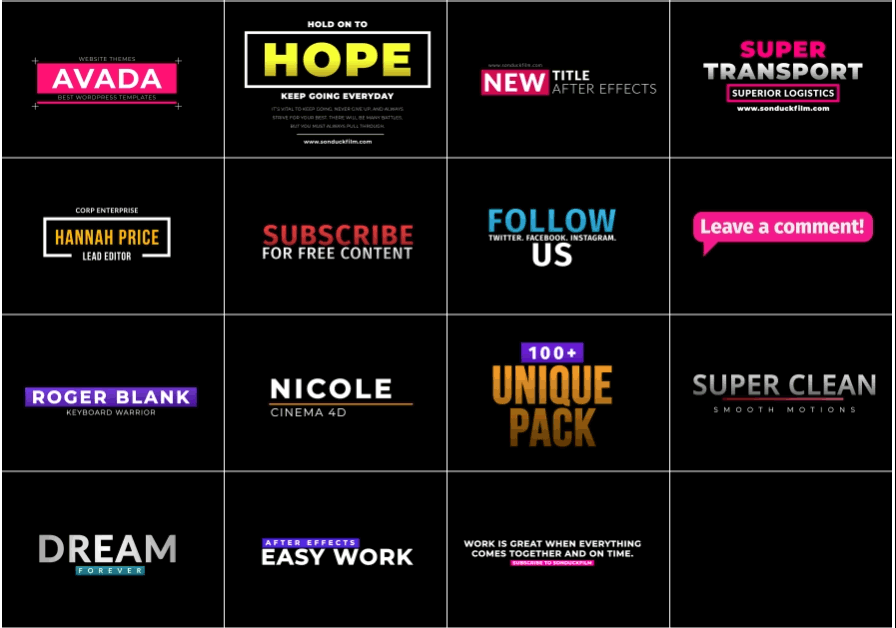

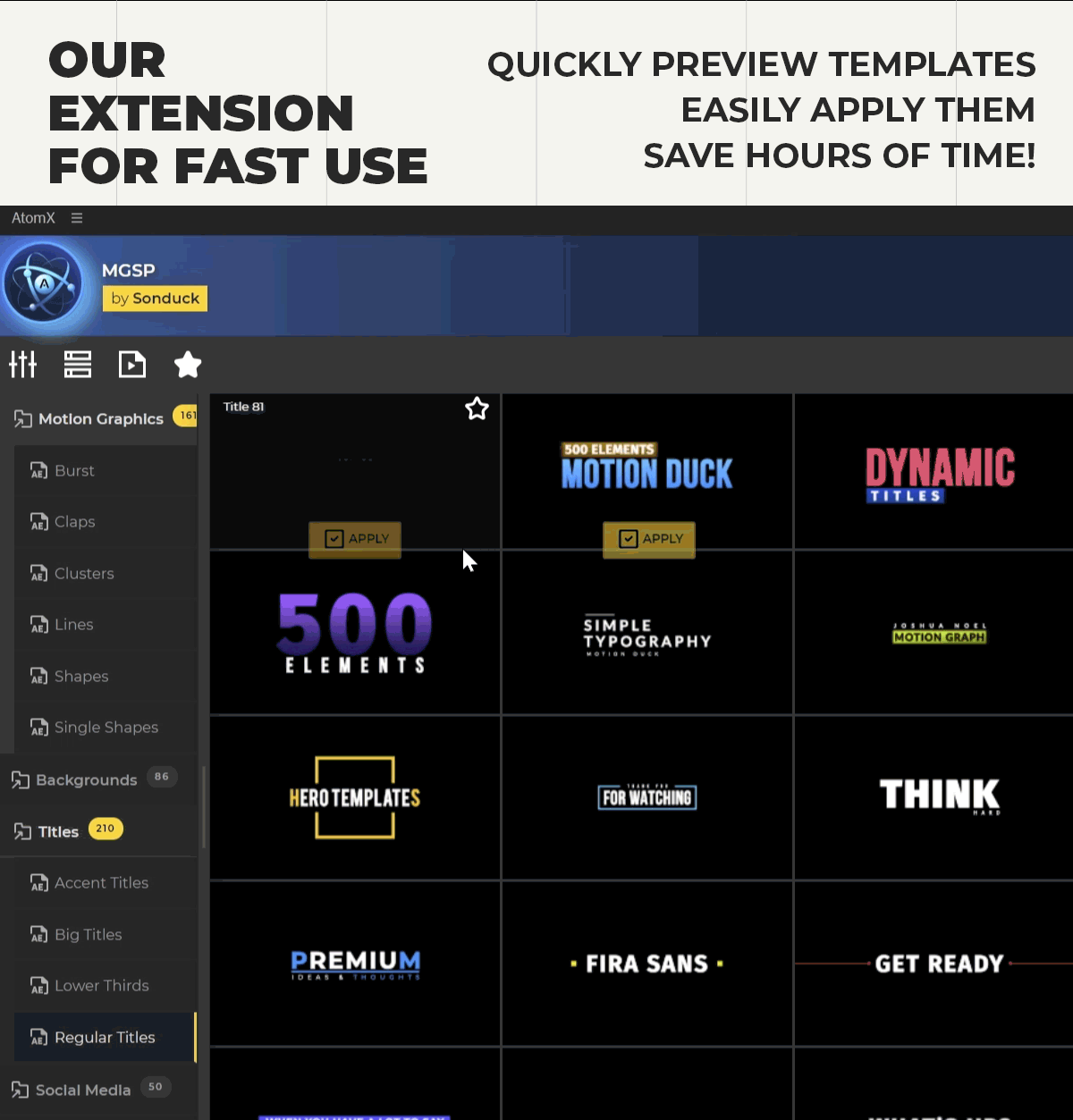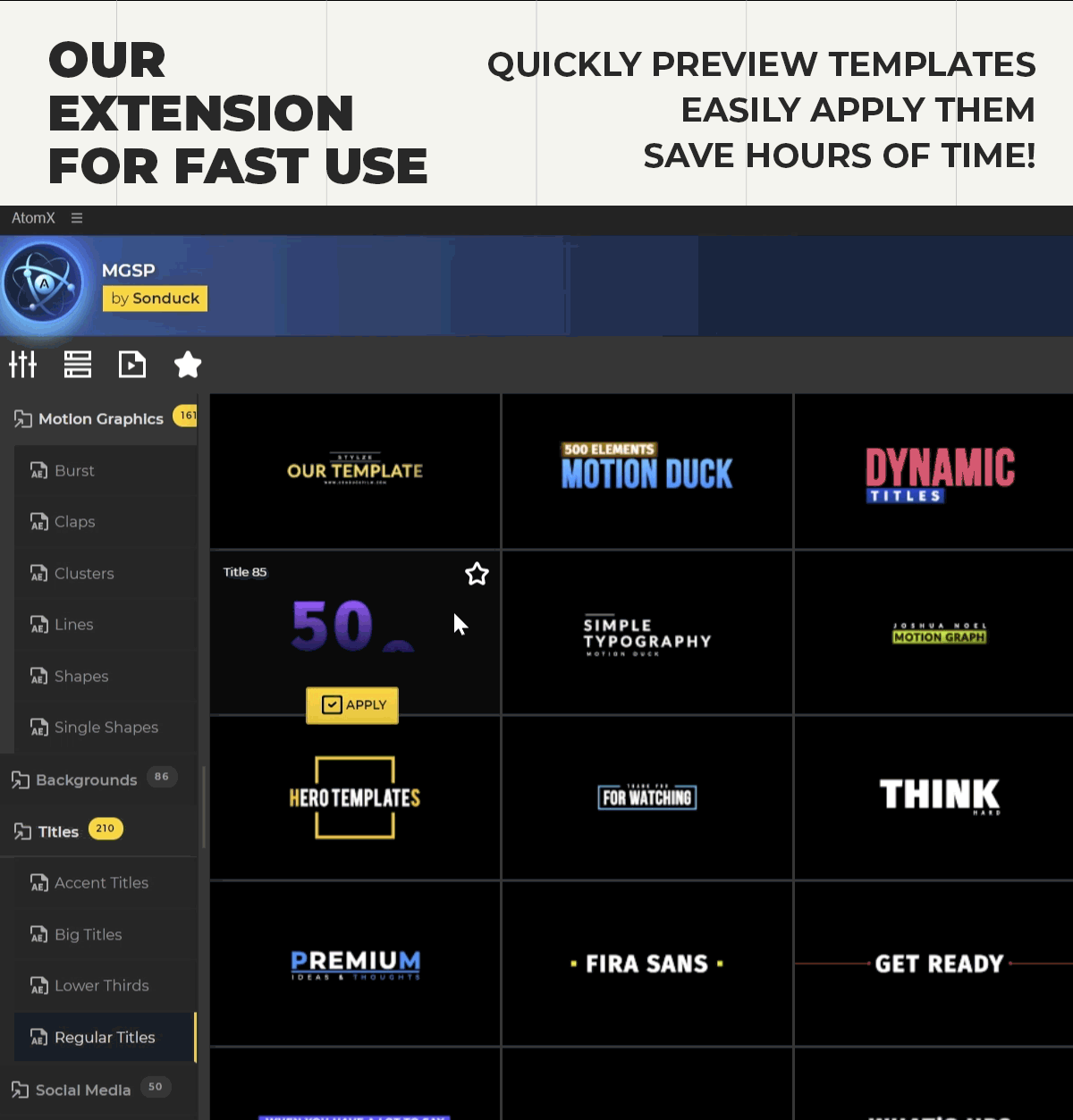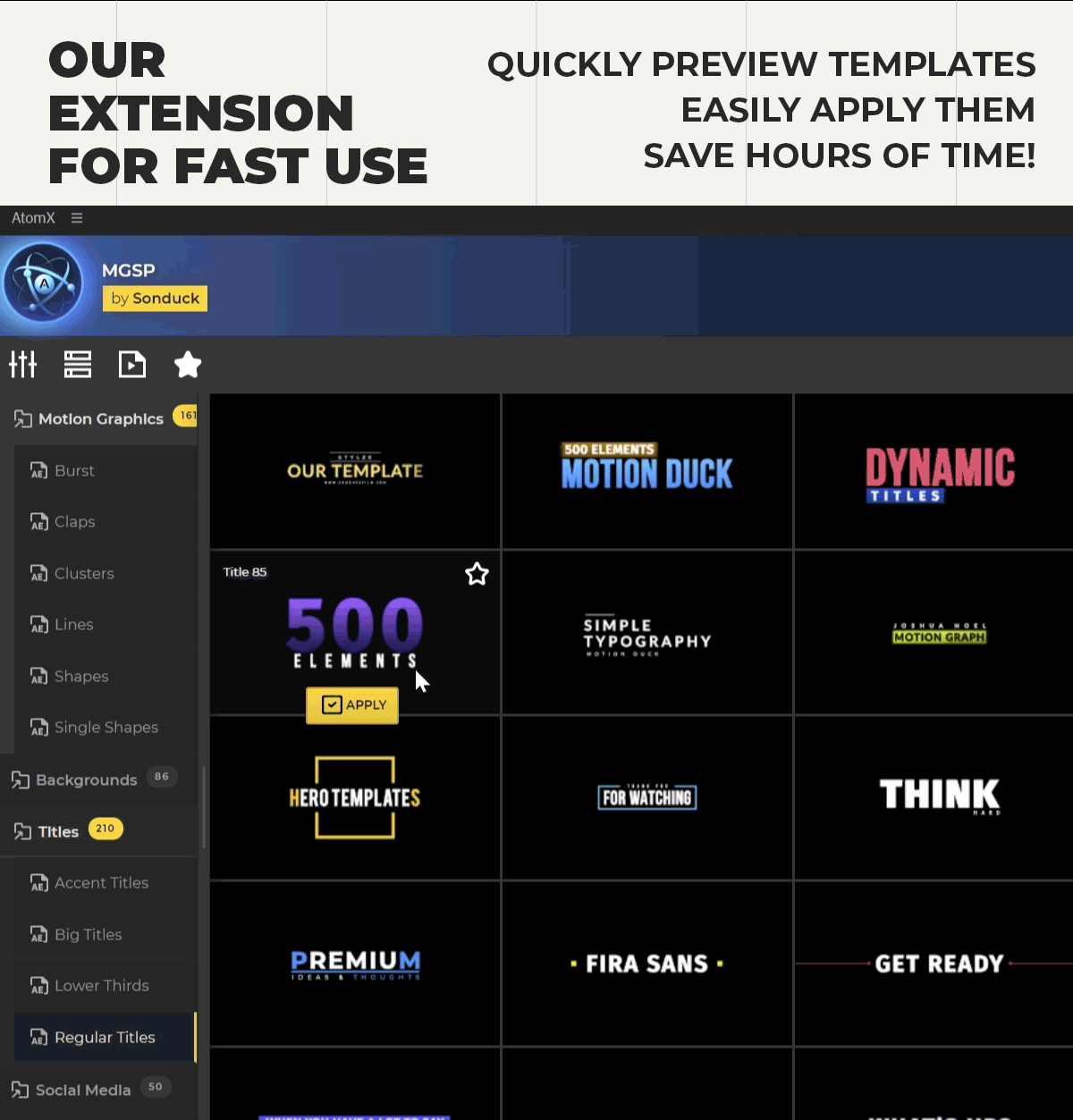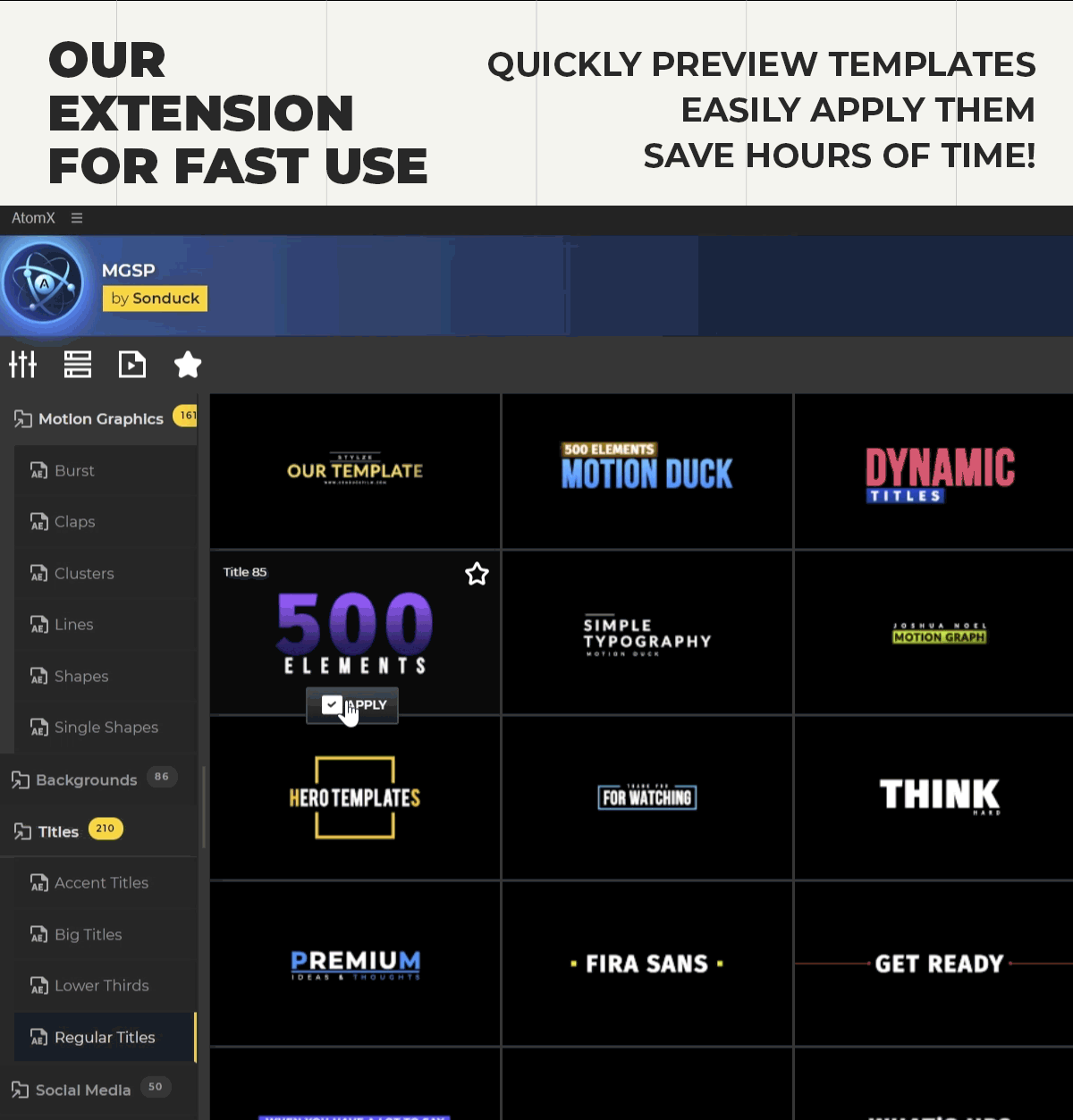
Features
-
- 42 beautifully animated motion graphics elements to use in your projects.
- 15 Accent Motion Graphics
- 15 Title Templates
- 12 Animated Backgrounds
- Full After Effects Extension
- 1920×1080
- Works with any FPS
- After Effects CC 2017 and Above
- Lifetime “Unlimited” license for all your projects.
- Easily change the colors of every element.
- Drag and drop all elements quickly and easily into your compositions.
- Fast render.
- Fully customizable components and elements.
- Pre-Renders Accent Motion Graphics for fast editing and for Adobe Premiere
- No plugins.
- No footage or images.
- Perfect for titles, intros, explainer videos and design projects.
- Simple, clean designs, to use very quickly and easily!









you are the best 🙂
Thanks alot, you are awesome
right
Thanks sir
Thanks sir
Thanks so much
great noel wow your the best bro
Thank u sir
thank u sir
thanks alot sir
thanks sir
thank you you are best guy!
Great man
you are the best Joshua Noel
Happy New Year
Thank You Sir, I am so greatful for your kindness in sharing your knowledge and resources.
Thanks Josh! Happy 2021
Happy New Year… and thanks for sharing !!
Thank you Sir
Thanks a lot bro I really appreciate.
Thanks SonduckFilm
Thanks sir your my inspiration sir
Thanks again Josh,
Your YouTube Channel ROCKS!. CHeers! Happy 2021
Amazing thank you!!
thank you!!
nice one
Awesome pack.
What’s the font for the pack please?
Joshua, you are an awesome man. thank’s
thank you
Grato Joshua, vou testar este pacote e assim que possivel vou comprar o pacote completo!
Thanks Josh.. Great job!
Thanks alot, you are awesome
Thank you…
thanks…
Thanks sir
Thank you bro
Thank you so much I learn AE from you every clip
God bless
Thank you so much!
Thanks! Bro.
THANKS ALOT PRO
MUCHAS GRACIAS…
i love to follow you as the explanation you give is easy to follow
Thank you so much!?
Thank you!
Thnku so much
From Syria we love you
Thanks! Excelent job!
You’re just awesome